| respondent_id | life_satisfaction | country | unemployed_active |
|---|---|---|---|
| 10608 | 5 | FR | 0 |
| 10405 | 8 | FR | 1 |
| 10007 | 7 | FR | 0 |
| 11170 | 10 | FR | 0 |
| 10751 | 10 | FR | 1 |
| 10005 | 10 | FR | 0 |
| .. | .. | .. | .. |
Machine learning: Fundamental concepts
Chapter last updated: 12 Februar 2025
Learning outcomes/objective: Learn…
- …about logic underlying predictive models.
- …about mean as a predictive model.
- …training, validation and test data.
- …about regression vs. classification.
- …assessing model accuracy.
- …the machine learning workflow.
- …prediction models (general form) as well as bias/variance trade-off
- …compontents of tidymodels
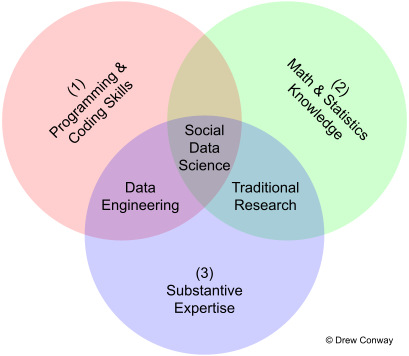
1 Predictive modelling: Skills
2 Mean as a ‘predictive model’
2.1 Mean as a model: Data (1)
- Data: European Social Survey (ESS): Round 10 - 2020. Democracy, Digital social contacts
- Measures of life satisfaction, unemployment etc. (cf. Table 1)
- We will use this data shown in Table 1 for our predictions later on!
2.2 Mean as a model (2)
- Model(s) = Mathematical equation(s)
- Underlying a model is always a (joint) distribution
- Model summarizes (joint) distribution with fewer parameters
- e.g. mean with one parameter
- e.g., linear model with three variables (\(y\), \(x1\), \(x2\)) with three parameters (\(\text{intercept }\beta + \beta_{1} + \beta_{2}\))
- …we start with a simple example!
- “using only information from the outcome variable itself for our prediction”
2.3 Mean as a model (3)
- Simple model: Mean of the distribution of a variable
\[ \begin{aligned} \text{Lifesatisfaction}_{Claudia} = 5 = \underbrace{\color{blue}{\overline{y}}}_{\color{green}{\widehat{y}}_{Claudia}} \pm \color{red}{\varepsilon}_{Claudia} = \color{blue}{7.03} \color{red}{-2.03} \end{aligned} \]
Mean (= model) predicts Claudia’s value with a certain error
Q: How well does the model (mean = 7) predict person’s that have values of 1, of 7.03 or of 8? What is the bias?
Important: We could use this model – this mean – to predict…
- …life_satisfaction values of people that gave no answer (missings in the dataset)
- …life_satisfaction values of another group of people, e.g., Germans
- …future life_satisfaction values of other or the same people
Here the outcome variable has values from 0-10. The mean for a binary outcome variable is simply the share of 1s, e.g., in the data above the share (mean) of unemployed actively looking for a job (France) is 0.04 (73 out of 1977).
2.4 Mean as a model (table) (4)
- In Table 2 we added our predictions to the data showing only the first ten lines of the dataset (see column “error”)
- Mean provides same prediction \((\hat{y})\) for everyone
| Name | life_satisfaction | prediction (mean) | error |
|---|---|---|---|
| Emily | 10 | 7.034 | 2.966 |
| Angel | 7 | 7.034 | -0.034 |
| Victoria | 7 | 7.034 | -0.034 |
| Ashtyn | 5 | 7.034 | -2.034 |
| Eduardo | 7 | 7.034 | -0.034 |
| Dustin | 10 | 7.034 | 2.966 |
| Tristin | 8 | 7.034 | 0.966 |
| Brandyn | 8 | 7.034 | 0.966 |
- Qs
- What are the (dis-)advantages of taking the mean as a predictive model? Is it a good predictive model?
- How could we assess whether the mean is a good predictive model? Do we need training and test data for that?
- In how for does the data determine whether the mean is a good predictive model?
Answer
- Q1
- Advantages: Simple, fast, works with sparse information (outcome only)
- Disadvantages: Potentially very biased/large errors
- Q2
- e.g., we can calculate the mean absolut error \((MAE)\)
- \(MAE = \frac{\sum_{i}^{n} |y_{i} - x_{i}|}{n} = \frac{\sum_{i}^{n} |\epsilon_{i}|}{n}\) where \(y_{i}\) = prediction, \(x_{i}\) = true value and \(n\) = total number of datapoints, \(\epsilon_{i}\) = error
- MAE = 1.69482
- How can we interprete the MAE?
- Yes, test data if we want to test how well the mean works for new unseen data
- e.g., we can calculate the mean absolut error \((MAE)\)
- Q3
- Mean can be very good if everyone lies close to the mean (e.g., mean age is 25 whereby all students are between 24 and 26 years old)
3 Training, validation and test dataset
3.1 Training, validation and test dataset
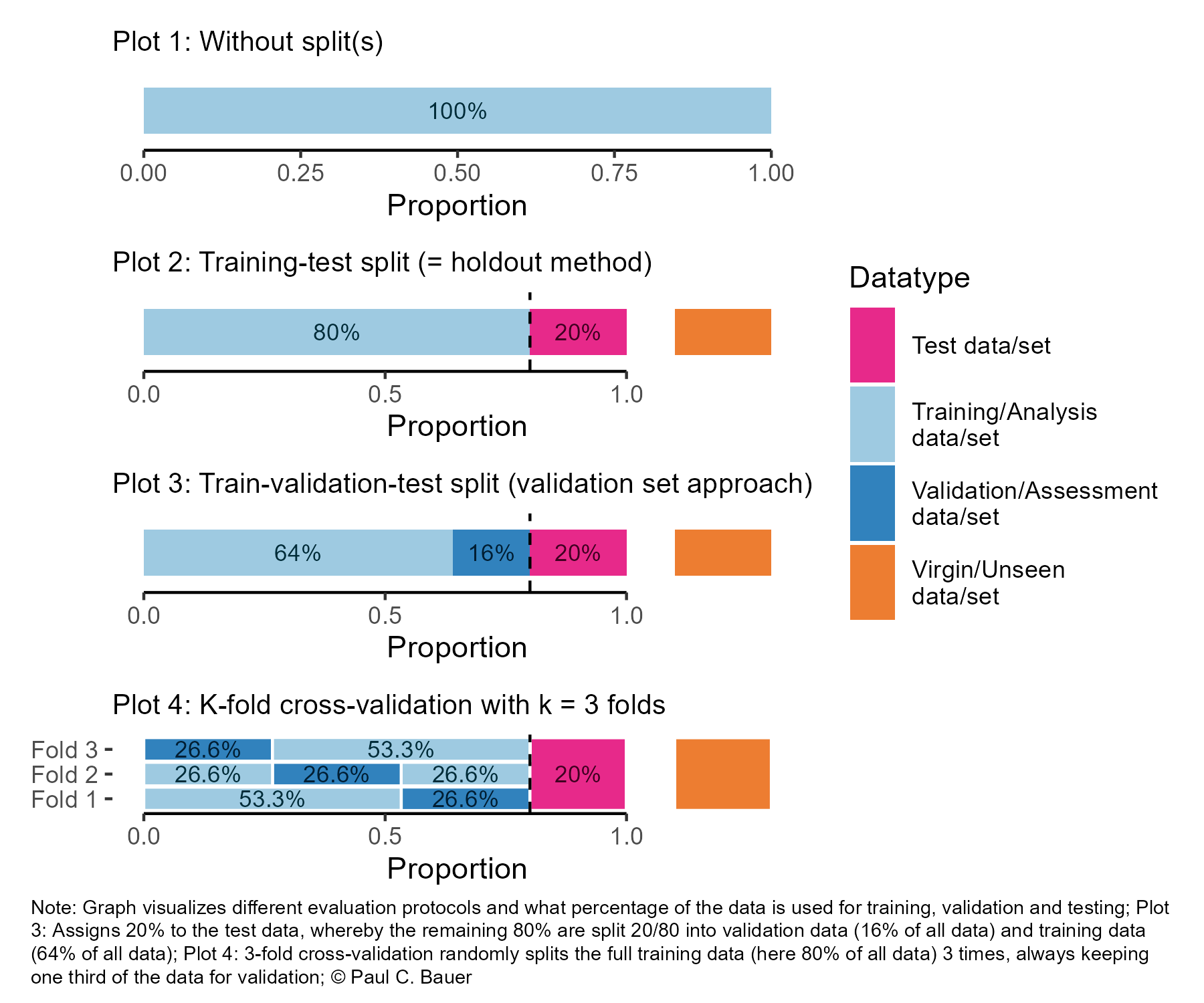
- As shown in Figure 2 when training models we sometimes…
- …only split into one training data subset, e.g., 80% of observations, and one test data subset, e.g., 20% of observations (cf. Plot 2)
- … introduce one further split (cf. Plot 3) - e.g., built models on training (analysis) dataset, validate/tune model using validation (assessment) dataset and use test dataset ONLY for final test
- …do resampling (see next slide!)
- As indicated in Figure 2, Plot 3 when doing further splitting the training data we can use the terms analysis and assessment dataset (Max Kuhn and Johnson 2019) (see also next slide)
3.2 Training, validation and test dataset: Resampling (several splits/folds)
- To avoid conceptual confusion we use the terminology by Max Kuhn and Johnson (2019) and illustrated in Figure Figure 3
- Datasets obtained from the initial split are called training and test data
- Datasets obtained from further splits to the training data are called analysis (analysis) and assessment (validation) datasets
- Often such further splits are called folds.
3.3 Training, validation and test dataset (3)
- Size of datasets: Usually 80/20 splits but depends..
- Q: What could be a problem if training and/or test dataset is too small? (uncertainty, representativeness)
Answer
- Training data ↓ → Variance of parameter estimates ↑
- Test data ↓ → Variance of performance statistic ↑
4 Exercise: What’s predicted?
- Q: What do we predict using the techniques below? What is the input/what is the output? How could we use those ML models for research in our disciplines? (discuss 2!)
Answer
- Image recognition: Predict whether an image shows a sunsetSome examples
- Speech recognition: Predict which (written) words someone just used
- Translation: Predict which English word/sentence corresponds to a German word/sentence (predict language!)
- Text analysis/Natural language processing (NLP): Predict entities, sentiment, syntax, categories in text
- Pose estimation (2018!): Predict body pose from image (predict where body parts are)
- Deepart: “Predict” what an image would look like if it was painted by…
- Deep fakes (2019): ?
5 Regression vs. Classification
Variables can be characterized as either quantitative or qualitative (= categorical)
Quantitative variables: Numerical values, e.g., person’s age, height, or income,
Qualitative variables: Values in one of K different classes, or categories
- e.g., a person’s gender (male or female)
Q: Are the following variables quantitative (A) or qualitative (B)?
- brand of product purchased, (2) wether a person defaults on a debt, (3) value of a house, (4) cancer diagnosis (Acute Myelogenous Leukemia, AcuteLymphoblastic Leukemia, or No Leukemia), (5) price of a stock
Problems with quantitative response = regression problems
Problems with qualitative response = classification problems
Distinction is not always crisp, e.g., logistic regression
- Typically used with a qualitative (two-class, or binary) response
- But estimates are class probabilities
Source: James et al. (2013, chap. 2.1.5)
5.1 Exercise: Classification or regression?
Classification problems occur often, perhaps even more so than regression problems, e.g., :
- A person arrives at the emergency room with a set of symptoms that could possibly be attributed to one of three medical conditions. Which of the three conditions does the individual have?
- An online banking service must be able to determine whether or nota transaction being performed on the site is fraudulent, on the basis of the user’s IP address, past transaction history, and so forth.
- On the basis of DNA sequence data for a number of patients with and without a given disease, a biologist would like to figure out which DNA mutations are deleterious (disease-causing) and which are not.
If we have a set of training observations (\(x_{1},y_{1}\)),…,(\(x_{n},y_{n}\)), we can build a classifier
Why not linear regression?
- No natural way to convert qualitative response variable with more than two levels into a quantitative response for LM
- e.g., 1 = stroke, 2 = drug overdose, 3 = epileptic seizure
- and linear probability model for binary outcome provides predictions outside of [0,1] interval (James et al. 2013, 131, Figure 4.2)
- No natural way to convert qualitative response variable with more than two levels into a quantitative response for LM
Source: James et al. (2013, chaps. 4.1, 4.2)
5.2 Classification: Two-class (binary) vs. multi-class problems
- Many classification involve several classes…
- …but can usually be reframed as (multiple) two-class
- e.g., Religion: Predicting whether someone is protestant vs. all others
- Logistic regression restricted to two-class problems by default
- Other models allow for predicting several classes (e.g., multinomial logistic regression)
6 Assessing Model Accuracy
6.1 Assessing Model Accuracy: Classification
- Accuracy or Correct Classification Rate (CCR), i.e., the rate of correctly classified test observations
- …the opposite of the error rate
- Training error rate: the proportion of mistakes that are made if we apply estimate to the training observations
- \(\frac{1}{n}\sum_{i=1}^{n}I(y_{i}\neq\hat{y}_{i})\): Fraction of incorrect classifications
- \(\hat{y}_{i}\): predicted class label for observation \(i\)
- \(I(y_{i}\neq\hat{y}_{i})\): indicator variable that equals 1 if \(y_{i}\neq\hat{y}_{i}\) (= error) and zero if \(y_{i}=\hat{y}_{i}\)
- If \(I(y_{i}\neq\hat{y}_{i})=0\) then the ith observation was classified correctly (otherwise missclassified)
- \(\frac{1}{n}\sum_{i=1}^{n}I(y_{i}\neq\hat{y}_{i})\): Fraction of incorrect classifications
- Test error rate: Associated with a set of test observations of the form (\(x_{0},y_{0}\))
- \(\frac{1}{n}\sum_{i=1}^{n}I(y_{0}=\hat{y}_{0})\)
- \(\hat{y}_{0}\): predicted class label that results from applying the classifier to the test observation with predictor \(x_{0}\)
- \(\frac{1}{n}\sum_{i=1}^{n}I(y_{0}=\hat{y}_{0})\)
- Good classifier: One for which the test error rate is smallest
- Further measures: Precision, recall (sensitivity), F1 score, ROC AUC
- We will discuss those in a later section!
- Source: James et al. (2013, chap. 2.2.3)
More background
We’ll discuss the measures below once we talk more deeply about classification in a later section!
- Accuracy:
- Accuracy measures the proportion of correctly classified instances among the total instances.
- It is calculated as the number of correctly predicted instances divided by the total number of instances.
- Accuracy is a simple and intuitive metric, but it can be misleading, especially in imbalanced datasets where the classes are not evenly represented.
- Precision:
- Precision measures the proportion of true positive predictions among all positive predictions.
- It is calculated as the number of true positive predictions divided by the sum of true positive and false positive predictions.
- Precision focuses on the accuracy of positive predictions and is useful when the cost of false positives is high.
- Recall (Sensitivity):
- Recall measures the proportion of true positive predictions among all (actual) positive instances.
- It is calculated as the number of true positive predictions divided by the sum of true positive and false negative predictions.
- Recall focuses on capturing all positive instances and is important when the cost of false negatives is high.
- F1 Score:
- F1 score is the harmonic mean of precision and recall.
- It provides a balance between precision and recall, especially when there is an imbalance between the classes.
- F1 score is calculated as the harmonic mean of precision and recall: \(F1 = 2 \times \frac{precision \times recall}{precision + recall}\).
- F1 score ranges from 0 to 1, where 1 indicates perfect precision and recall, and 0 indicates poor performance.
- Accuracy and receiver operating characteristic area under the curve (ROC AUC) often used for balanced-classification problems and precision-recall for class-imbalanced problems. Ranking problems or multilabel classification may require other measures.
6.2 Assessing Model Accuracy: Regression
- Mean squared error (James et al. 2013, Ch. 2.2)
- \(MSE=\frac{1}{n}\sum_{i=1}^{n}(y_{i}- \hat{f}(x_{i}))^{2}\) (James et al. 2013, Ch. 2.2.1)
- \(y_{i}\) is \(i\)s true outcome value
- \(\hat{f}(x_{i}) = \hat{y}_{i}\) is the prediction that \(\hat{f}\) gives for the \(i\)th observation
- MSE is small if predicted responses are to the true responses, and large if they differ substantially
- \(MSE=\frac{1}{n}\sum_{i=1}^{n}(y_{i}- \hat{f}(x_{i}))^{2}\) (James et al. 2013, Ch. 2.2.1)
- Training MSE: MSE computed using the training data
- Test MSE: How is the accuracy of the predictions that we obtain when we apply our method to previously unseen test data?
- \(\text{Ave}(y_{0} - \hat{f}(x_{0}))^{2}\): the average squared prediction error for test observations \((y_{0},x_{0})\)
- Further measures
- Mean absolute error (MAE): …no squaring as in MSE but absolute values
- R-squared: See Definitions -> Figure
- Root mean squared error (RMSE): the square root of the MSE1
- Fundamental property of ML (cf. James et al. 2013, 31, Figure 2.9)
- As model flexibility increases, training MSE will decrease, but the test MSE may not
- Q: Why? (Hint: overfitting)
- As model flexibility increases, training MSE will decrease, but the test MSE may not
More background
- Difference Between MSE, MAE, and R-squared in Prediction Accuracy: MSE is suitable for applications where larger errors need to be penalized more, MAE is preferable when the emphasis is on the overall accuracy without sensitivity to outliers, and R-squared is useful for assessing the overall goodness of fit of the model. However, it’s often recommended to use multiple metrics together to get a comprehensive understanding of model performance.
- Mean Squared Error (MSE):
- MSE calculates the average squared difference between the actual values and the predicted values.
- It emphasizes larger errors due to the squaring operation, making it sensitive to outliers.
- It is differentiable, making it useful for optimization algorithms.
- It penalizes large errors more than smaller ones, which may not always be desirable depending on the application.
- MSE can be heavily influenced by outliers, making it less robust in the presence of outliers.
- Mean Absolute Error (MAE):
- MAE calculates the average absolute difference between the actual values and the predicted values.
- It provides a more balanced view of errors compared to MSE as it is not as sensitive to outliers.
- It is more interpretable than MSE since it’s in the same units as the original data.
- It treats all errors equally regardless of their magnitude, which may not reflect the actual importance of errors in some cases.
- MAE is not differentiable at zero, which can complicate optimization tasks.
- R-squared (Coefficient of Determination):
- R-squared measures the proportion of the variance in the dependent variable that is predictable from the independent variables.
- It provides an indication of the goodness of fit of the model.
- R-squared ranges from 0 to 1, where 1 indicates perfect prediction and 0 indicates no improvement over a baseline model (usually the mean of the dependent variable).
- It is scale-independent, making it easier to compare models across different datasets.
- R-squared can be misleading when used alone, especially with complex models, as it can increase even when adding irrelevant predictors (overfitting).
- It assumes that the relationship between the dependent and independent variables is linear, which may not always be the case.
6.3 Assessing Model Accuracy: Exercise on MSE, MAE
| Name | life_satisfaction | prediction (mean) | error |
|---|---|---|---|
| Emily | 10 | 7.75 | 2.25 |
| Angel | 7 | 7.75 | -0.75 |
| Victoria | 7 | 7.75 | -0.75 |
| Ashtyn | 5 | 7.75 | -2.75 |
| Eduardo | 7 | 7.75 | -0.75 |
| Dustin | 10 | 7.75 | 2.25 |
| Tristin | 8 | 7.75 | 0.25 |
| Brandyn | 8 | 7.75 | 0.25 |
In Table 3 you find data (only 8 observations, i.e., a subset of the data above) and (like above) we use the mean as a predictive model. * Please calculate the accuracy for those predictions (using error) by calculating both the MSE and the MAE. How would we proceed?2 (to make it simpler here are the values: c(2.25, -0.75, -0.75, -2.75, -0.75, 2.25, 0.25, 0.25))
Solution(s)
- MSE: Below tables with the calculation steps for the MSE
- Square the errors
- Sum up the squared errors & count observations
- Divide sum of squared errors by number of observations
| Name | life_satisfaction | prediction (mean) | error | error_squared |
|---|---|---|---|---|
| Emily | 10 | 7.75 | 2.25 | 5.0625 |
| Angel | 7 | 7.75 | -0.75 | 0.5625 |
| Victoria | 7 | 7.75 | -0.75 | 0.5625 |
| Ashtyn | 5 | 7.75 | -2.75 | 7.5625 |
| Eduardo | 7 | 7.75 | -0.75 | 0.5625 |
| Dustin | 10 | 7.75 | 2.25 | 5.0625 |
| Tristin | 8 | 7.75 | 0.25 | 0.0625 |
| Brandyn | 8 | 7.75 | 0.25 | 0.0625 |
| n | error_squared_sum | MSE |
|---|---|---|
| 8 | 19.5 | 2.4375 |
- MAE: Below tables with the calculation steps for the MAE
- Get absolute values of errors
- Sum up the absolute values of errors & count observations
- Divide sum of absolute values of errors by number of observation
| Name | life_satisfaction | prediction (mean) | error | error_absolute |
|---|---|---|---|---|
| Emily | 10 | 7.75 | 2.25 | 2.25 |
| Angel | 7 | 7.75 | -0.75 | 0.75 |
| Victoria | 7 | 7.75 | -0.75 | 0.75 |
| Ashtyn | 5 | 7.75 | -2.75 | 2.75 |
| Eduardo | 7 | 7.75 | -0.75 | 0.75 |
| Dustin | 10 | 7.75 | 2.25 | 2.25 |
| Tristin | 8 | 7.75 | 0.25 | 0.25 |
| Brandyn | 8 | 7.75 | 0.25 | 0.25 |
| n | error_absolute_sum | MSA |
|---|---|---|
| 8 | 10 | 1.25 |
6.4 Assessing Model Accuracy: Exercise on error rate
In Table 4 you find data (only 8 observations, i.e., a subset of the data above) and (like above) we use the mean as a predictive model. Please assess the accuracy for those predictions for the dataset by calculating the error rate. How would we proceed? (to make it simpler here are the values: c(1, 1, 1, 1, 1, 1, 1, 1) or calculate it in your head!)
| Name | unemployed | prediction (mean) | prediction (binary) |
|---|---|---|---|
| Connor | 0 | 0.5 | 1 |
| Shaahida | 0 | 0.5 | 1 |
| Cynthia | 0 | 0.5 | 1 |
| Zuhair | 1 | 0.5 | 1 |
| Chykeiljah | 0 | 0.5 | 1 |
| Dinah | 1 | 0.5 | 1 |
| Michael | 1 | 0.5 | 1 |
| Dameion | 1 | 0.5 | 1 |
Solution
- Below tables with the calculation steps for the error rate
- Get binary prediction. Usually cutoffs are \(p > 0.5 \rightarrow 1\) \(p<0.5 \rightarrow 0\), were \(p\) is the predicted probability. Here when taking the mean as predicted probability all are predicted to be 0 (employed).
- Get incorrect classifications by comparing predicted with true values (1 = incorrect, 0 = correct)
- Sum up incorrect classifications & count observations
- Divide sum of incorrect classifications by number of observations
| Name | unemployed | prediction (mean) | prediction (binary) | incorrect_classifications |
|---|---|---|---|---|
| Connor | 0 | 0.5 | 0 | 0 |
| Shaahida | 0 | 0.5 | 0 | 0 |
| Cynthia | 0 | 0.5 | 0 | 0 |
| Zuhair | 1 | 0.5 | 0 | 1 |
| Chykeiljah | 0 | 0.5 | 0 | 0 |
| Dinah | 1 | 0.5 | 0 | 1 |
| Michael | 1 | 0.5 | 0 | 1 |
| Dameion | 1 | 0.5 | 0 | 1 |
| n | incorrect_classifications_sum | error_rate |
|---|---|---|
| 8 | 4 | 0.5 |
7 Universal workflow of machine learning
- Source: Adapted from Chollet and Allaire (2018, 118f)
- Define the problem at hand (outcome \(Y\) and features \(X\)) and the data on which you’ll be training. Collect this data, or annotate it with labels if need be.
- Choose how you’ll measure success on your problem. Which metrics will you monitor on your validation data? (e.g., \(MSE\), \(MAE\), Accuracy, etc.)
- Determine your evaluation protocol: hold-out validation? K-fold validation? Which portion of the data should you use for validation?
- Preparing/preprocess your data
- Develop a first model that does better than a basic baseline: a model with statistical power.
- Develop a model that overfits.
- Regularize your model and tune its hyperparameters, based on performance on the validation data.
- Final training (on all training + validation data) and model testing on test dataset
- Prediction of observations in virgin/unseen dataset
Often Step 5, 6, and 7 are subsumed under one step Training & validation.
8 Prediction models (general form)
8.1 Prediction: Model (general form)
- cf. James et al. (2013, 16–21)
- Output variable \(Y\), e.g., life satistfaction, trust, unemployment, recidivism
- Often called the response/dependent variable
- Input variable(s) \(X\) (usually with subscript, e.g., \(X_{1}\) is education)
- Usually called predictors/independent variables/features
- Example
- Quantitative response \(Y\) and \(p\) different predictors, \(X_{1},...,X_{p}\)
- We assume a relationship between output \(Y\) and inputs \(X = X_{1},...,X_{p}\)
- can be written generally as \(Y = f(X) + \varepsilon\)
- \(f\) represents the systematic information that \(X\) provides about \(Y\)
- \(\varepsilon\) is a random error term which is independent of \(X\) and has mean zero
- \(f\) is “true” function/model that produced \(Y\), e.g., the “true” function/model that produces life satisfaction given the inputs
- can be written generally as \(Y = f(X) + \varepsilon\)
8.2 Prediction: Why estimate \(f\) (model)?
Pertains to class distinction discussed in (Breiman 2001; James et al. 2013, 17–19)
Prediction: In many situations, a set of inputs \(X\) readily available, but true output values \(Y\) cannot be easily obtained, e.g., 20% of persons in a survey did not indicate their life satisfaction (missing data)
- In this setting, since the error term averages to zero, we can predict true values \(Y\) using \(\hat{Y} = \hat{f}(X)\)
- where \(\hat{f}\) represents our estimate for \(f\), and \(\hat{Y}\) represents the resulting prediction for \(Y\)
- \(f\) is “true” function that produced \(Y\), e.g., “true” function/model that produces life satisfaction
- \(f\) is often treated as a black box, i.e., typically we are less concerned with exact form of \(\hat{f}\) provided that the predictions are accurate
- In this setting, since the error term averages to zero, we can predict true values \(Y\) using \(\hat{Y} = \hat{f}(X)\)
Inference: Understand the relationship between \(Y\) and \(X\)3
8.3 Prediction: Accuracy
- Accuracy of \(\hat{Y}\) as prediction for \(Y\) depends on two quantities
- reducible error (introduced by innaccuracy of \(\hat{f}\)) and the irreducible error (associated with \(\varepsilon\))
- \(\hat{f}\) will not be a perfect estimate of \(f\) but introduce error
- This error is reducible because we can potentially improve the accuracy of \(\hat{f}\) by using the most appropriate statistical learning technique to estimate \(f\)
- But even with perfect estimate of \(f\) (estimate response with form \(\hat{Y} = f (X)\)) irreducible error remains because \(Y\) is also function of \(\varepsilon\) that cannot be predicted using \(X\)
- Variability associated with \(\varepsilon\) also affects predictions and is called irreducible error
- Q: Why is the irreducible error (always) larger than 0?
Answer
The quantity \(\varepsilon\) may contain unmeasured variables that are useful in predicting \(Y\): since we don’t measure them, \(f\) cannot use them for its prediction. The quantity may also contain unmeasurable variation (James et al. 2013, 18–19).
Irreducible error will always provide an upper bound on the accuracy of our prediction for Y. This bound is almost always unknown in practice since we may not have measured/know the necessary features/predictors. (James et al. 2013, 19)
8.4 Prediction: How Do We Estimate f?
- We estimate \(f\) using the training data (James et al. 2013, 21–24)
- Parametric methods with two-step approach (James et al. 2013, 21–24)
- Make assumption about the functional form of \(f\), or shape, e.g., linear model
- Train or fit the model, e.g., most common method for linear model is (ordinary) least squares
- “parametric” because assumpions about data distribution (e.g., linear) and reduces problem of estimating \(f\) down to estimating a set of parameters, e.g., coefficients of linear model
- Potential disadvantage
- the model we choose will usually not match the true unknown form of \(f\)
- if too far from true \(f\) then estimate will be poor
- Flexible models can fit many different function forms for \(f\) but require estimating more parameters but increase danger of overfitting (Q: Overfitting?)
- Non-parametric methods (e.g. random forests)
- Do not make explicit assumptions about the functional form of \(f\)
- Seek estimate of \(f\) that gets as close to the data points as possible without being too rough or wiggly
8.5 Trade-Off(s): Prediction Accuracy vs. Model Interpretability
- Some ML methods are more some are less flexible (shape of f), e.g., linear model
- James et al. (2013, 25), Fig. 2.7. provides an overview
- Q: Why would we ever choose to use a more restrictive method (less flexible) model instead of a very flexible approach?
Answer
- Inference: If main goal is inference, restrictive models are much more interpretable. Linear model may be a good choice since it will be quite easy to understand the relationship between \(Y\) and \(X_{1}, ..., X_{p}\)
- Prediction
- Worse predictions: High flexibility can also yield worse predictions because of overfitting (counterintuitive!)
- Interpretability: Debate around interpretable machine learning: Sometime we would like to know why a model predicts well (which features matter how much!)
9 Bias/variance trade-off and accuracy
Learning outcomes/objective: Learn/understand…
- …bias-variance trade-off.
9.1 Bias-variance trade-off
- See James et al. (2013, Ch. 2.2.2)
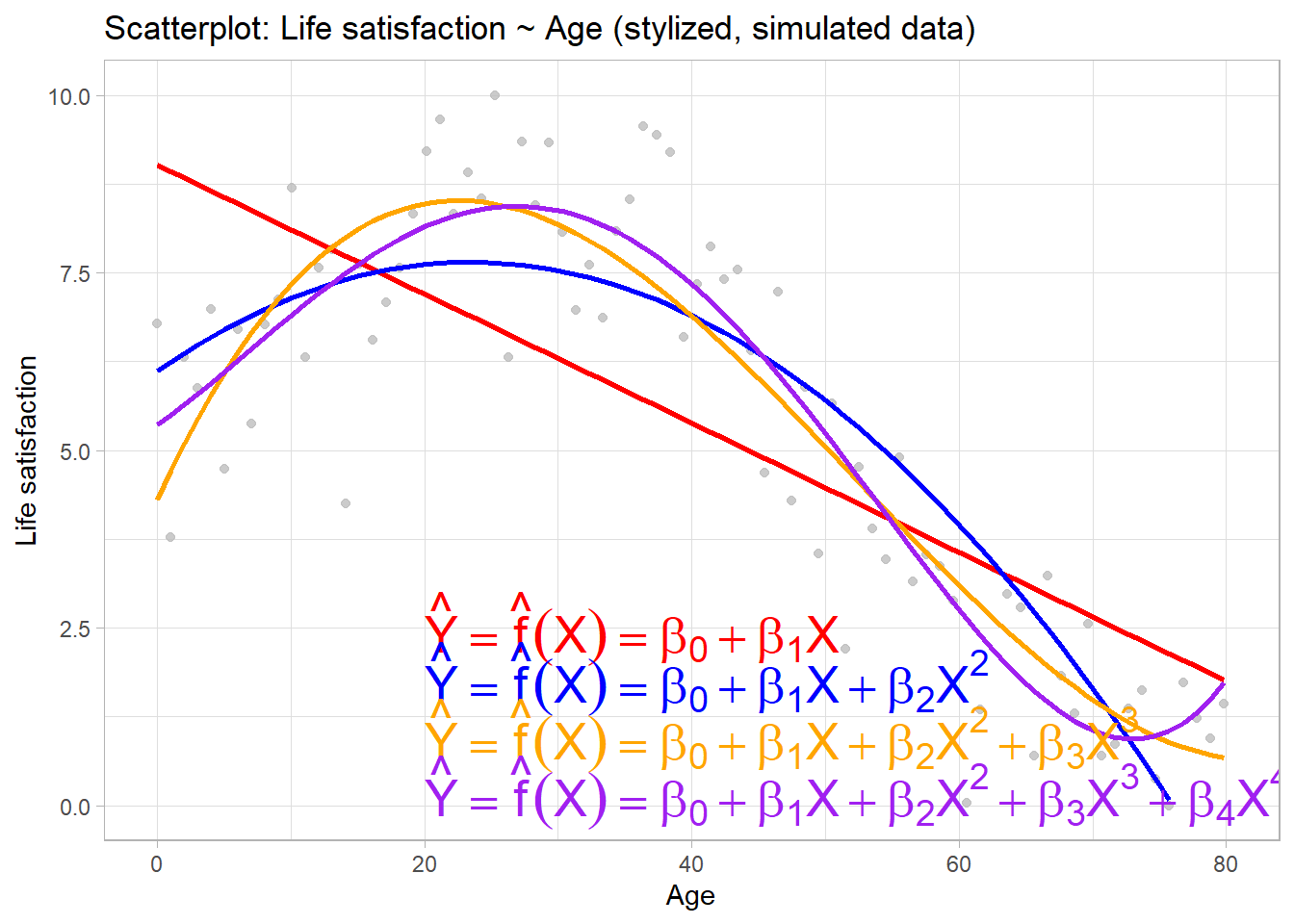
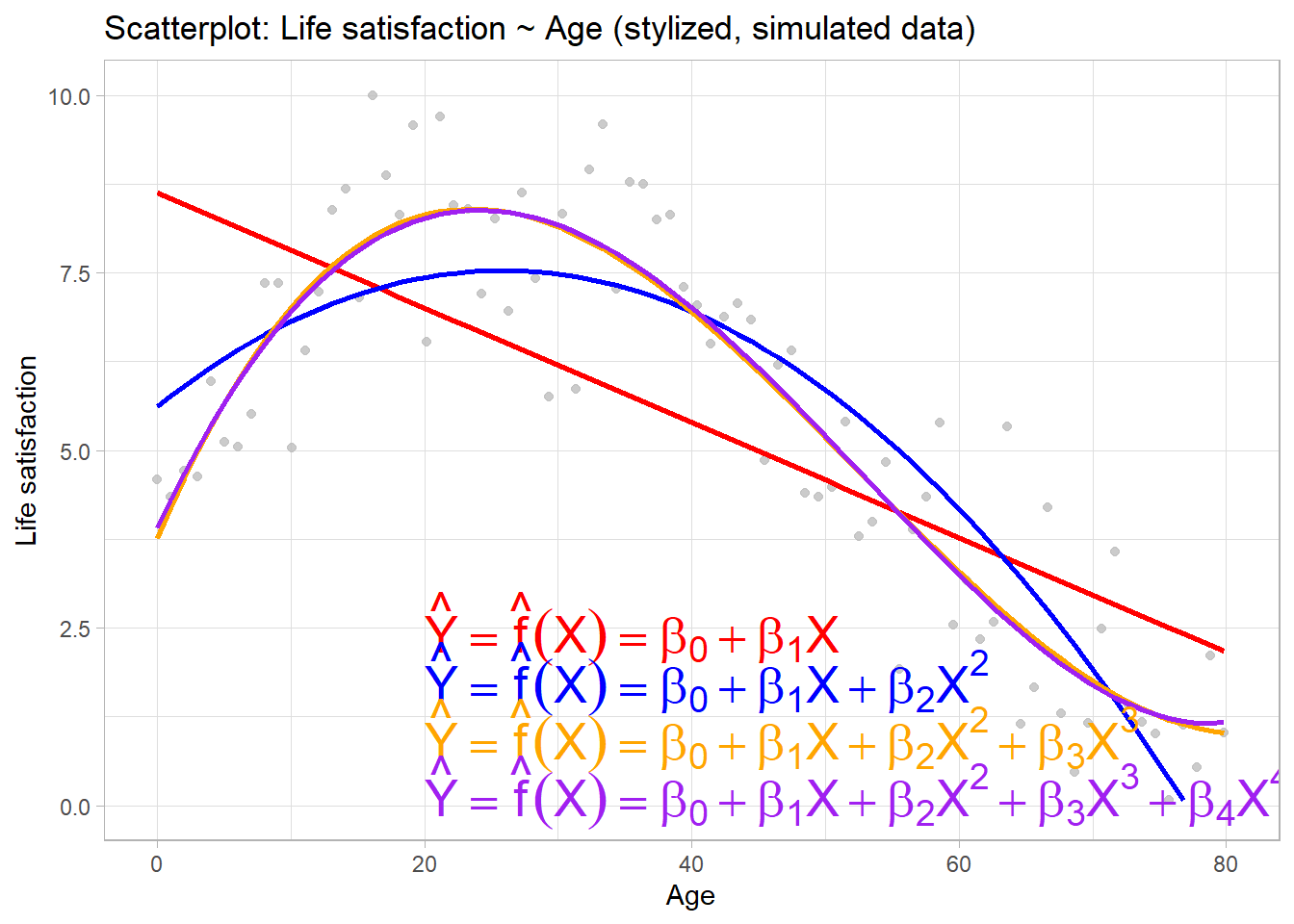
- Figure 5 shows an increasingly flexible model (linear model + polynomials)
9.1.1 Bias-variance trade-off (1)
- James et al. (2013) introduce bias-variance trade-off before turning to classification
- What do we mean by the variance and bias of a statistical learning method? (James et al. 2013, Ch. 2.2.2)
- Variance refers to amount by which \(\hat{f}\) would change if estimated using a different training data set
- Ideally estimate for \(f\) should not vary too much between training sets
- If method has high variance then small changes in training data can result in large changes in \(\hat{f}\)
- More flexible methods/models usually have higher variance
- Bias refers to the error that is introduced by approximating a (potentially complicated) real-life problem through a much simpler model (=\(f\))
- e.g., linear regression assumes linear relationship between \(Y\) and \(X_{1},X_{2},...,X_{p}\) but unlikely that real-life problems truly have linear relationship producing bias/error
- e.g., predict life satisfaction \(Y\) with age \(X\)
- If real-life \(f\) is substantially non-linear, linear regression will not produce accurate estimate \(\hat{f}\) of \(f\), no matter how many training observations
- Variance refers to amount by which \(\hat{f}\) would change if estimated using a different training data set
9.1.2 Bias-variance trade-off (2)
- Variance: error from sensitivity to small fluctuations in the training set
- High variance may result from an algorithm modeling the random noise in the training data (overfitting)
- Bias error: error from erroneous assumptions in the learning algorithm (\(\hat{f}\)) about \(f\)
- High bias can cause an algorithm to miss relevant relations between features and target outputs (underfitting)
- Bias-variance trade-off: Property of model that variance of parameter(s) estimated across samples can be reduced by increasing the bias in the estimated parameters
- e.g., we may choose linear model with higher bias to decreas variance
- Bias-variance dilemma/problem: Trying to simultaneously minimize these two sources of error that prevent supervised learning algorithms from generalizing beyond their training set
9.1.3 Bias-variance trade-off (3)
- “General rule”: with more flexible methods/models, variance will increase and bias will decrease
- Relative rate of change of these two quantities determines whether test MSE (regression problem) increases or decreases
- As we increase flexibility of a class of methods, bias tends to initially decrease faster than the variance increases
- Consequently, the expected test MSE declines as shown in Figure 6.
- Q: What does Figure 6 illustrate and which level of flexibility would be desirable?
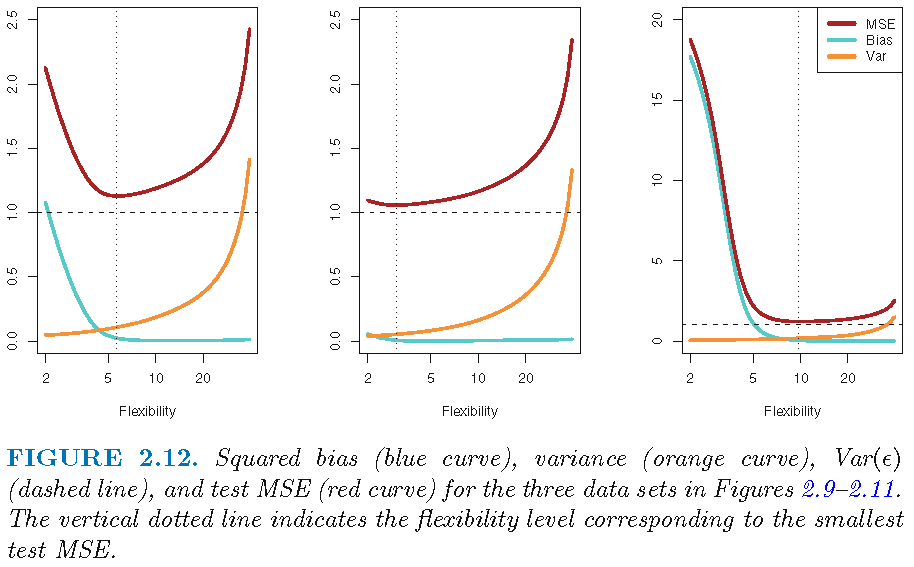
Answer
- Figure 6 visualizes squared bias, variance and MSE as a function of flexibility. We would normally pick a flexibility level that minimizes all three of them (indicated by the vertical dashed line).
9.1.4 Bias-variance trade-off (4)
- Good test set performance requires low variance as well as low squared bias
- Trade-off because easy to obtain method with…
- …extremely low bias but high variance
- e.g., just draw a curve that passes through every single training observation
- …very low variance but high bias
- e.g., by fitting a horizontal line to the data
- …extremely low bias but high variance
- Trade-off because easy to obtain method with…
- Challenge lies in finding a method for which both the variance and the squared bias are low
- This idea will return throughout the course!
- In real-life situation \(f\) is unobserved hence not possible to compute test MSE, bias, or variance for a statistical learning method (because we fit our model to the training data not the test data!)
- But good to keep in mind and later on we discuss methods to estimate test MSE using training (cross-validation!)
9.2 Exercise 1
Adapted from James et al. (2013, Exercise 2.4.1): Thinking of our classification problem (predicting recidivism, i.e., whether a prisoner reoffends), indicate whether we would generally expect the performance of a flexible statistical learning method to be better or worse than an inflexible method. Justify your answer.
- The sample size \(n\) is extremely large, and the number of predictors \(p\) is small.
- The number of predictors \(p\) is extremely large, and the number of observations \(n\) is small.
- The relationship between the predictors and response is highly non-linear.
- The variance of the error terms, i.e. \(\sigma^{2}=Var(\epsilon)\), is extremely high.
Answer
- Flexible is better since there is less room for adaption to outliers!
- Flexible is worse since function will adapt non-typical outliers!
- Flexible is better because the function should adapt the non-linear true function f.
- Flexible is probably better because it would better adapt to the high variance, i.e., high variance seems to indicate that non-flexible model is not a good approximation of f.
9.3 Exercise 2
James et al. (2013, Exercise 2.4.2): Explain whether each scenario is a classification or regression problem, and indicate whether we are most interested in inference or prediction. Finally, provide \(n\) and \(p\).
- We collect a set of data on the top 500 firms in the US. For each firm we record profit, number of employees, industry and the CEO salary. We are interested in understanding which factors affect CEO salary.
- We are considering launching a new product and wish to know whether it will be a success or a failure. We collect data on 20 similar products that were previously launched. For each product we have recorded whether it was a success or failure, price charged for the product, marketing budget, competition price, and ten other variables.
- We are interesting in predicting the % change in the US dollar in relation to the weekly changes in the world stock markets. Hence we collect weekly data for all of 2012. For each week we record the % change in the dollar, the % change in the US market, the % change in the British market, and the % change in the German market.
Answer
- Regression problem; Inference; n = 500; p = 3 (profit, number of employees, industry)
- Classification problem; Prediction; n = 20; p = 14 (success or failure, price charged for the product, marketing budget, competition price, and ten other variables)
- Regression problem; Prediction; n = 52; p = 4; (% change in the dollar, the % change in the US market, the % change in the British market, and the % change in the German market)
10 Tidymodels & packages

- See github website.
10.1 Overview of packages
- A collection of packages for modeling and machine learning using tidyverse principles (see Barter (2020), M. Kuhn and Wickham (2020) and M. Kuhn and Silge (2022) for summaries)
- Much like
tidyverse,tidymodelsconsists of various core packages:rsample: for sample splitting (e.g. train/test or cross-validation)- provides functions to create different types of resamples and corresponding classes for their analysis
initial_split: Use this to split the data into training and test data (with argumentsprop,strata)prop-argument: Specify share of training data observationsstrata-argument: Conduct stratified sampling on the dependent variable (better if classes are imbalanced!)training(),testing(),analysis()andassessment()can be used to extract the corresponding datasets from anrsplitobjectvalidation_split: Split the training data into analysis data (= training data) and assessment data (= validation data)- Later we’ll explore more functions such as
vfold_cv
- Later we’ll explore more functions such as
recipes: for pre-processing- Use dplyr-like pipeable sequences of feature engineering steps to get your data ready for modeling.
parsnip: specifying the model namely model type, engine and mode- Goal: provide a tidy, unified interface to access models from different packages
model type-argument: e.g, linear or logistic regressionengine-argument: R packages that contain these modelsmode-argument: either regression or classification
tune: for model tuning- Goal: facilitate hyperparameter tuning. It relies heavily on
recipes,parsnip, anddialsdials: contains infrastructure to create and manage values of tuning parameters
- Goal: facilitate hyperparameter tuning. It relies heavily on
yardstick: evaluate model accuracy- Goal: estimate how well models are working using tidy data principles
conf_mat(): calculates cross-tabulation of observed and predicted classesconf_mat() %>% pluck("table") %>% t() %>% addmargins(): Flip and add margins
metrics(): estimates 1+ performance metrics
workflowsets:- Goal: allow users to create and easily fit a large number of different models.
- Use
workflowsetsto create aworkflow setthat holds multipleworkflow objects- These objects can be created by crossing all combinations of preprocessors (e.g., formula, recipe, etc) and model specifications. This set can be tuned or resampled using a set of specific functions.
10.2 ML workflow using tidymodels
| Data resampling, feature engeneering | Model fitting, tuning | Model evaluation |
|---|---|---|
| rsample | tune | yardstick |
| recipes | parsnip | |
| dials |
References
Footnotes
The units of RMSE are the same as the units of the target variable. So, if you’re predicting house prices in dollars, the RMSE will also be in dollars.↩︎
Importantly, while we have only one dataset here and the mean model is based on this dataset, in ML applications the model is estimated based on some training data and the accuracy assessed with another dataset namely validation or test data↩︎
See corresponding questions in James et al. (2013, 19–20)↩︎